Historic and conceptual background
Modeling spatial interactions
Modeling spatial interactions is used to understand and quantify the
level of interaction between different locations.
The most ancient and common spatial interactions model the gravity
model. It has roots in the late 19st century and has been used in
several fields (geography, economy, demography) to model a high variety
of flows (commuting, trade, migrations). A brief presentation can be
found in Rodrigue, Comtois, and Slack
(2013) and a more detailed one, among many others, in Fotheringham and O’Kelly (1989).
A place-based model: Stewart’s potentials
There are two main ways of modeling spatial interactions: the first
one focuses on links between places (flows), the second one focuses on
places and their influence at a distance. Following the physics
metaphor, the flow may be seen as the gravitational
force between two masses, the place influence as the
gravitational potential. The potential
package, as its name suggests, proposes an implementation of the
place-based model of potential defined by John Q. Stewart (1941).
The Stewart model is also known in the literature, depending on the discipline, as potential access, gravitational potential or gravitational accessibility. The concept was developed in the 1940s by physicist John Q. Stewart from an analogy to the gravity model. In his seminal work on the catchment areas of American universities, Stewart computes potentials of population. This potential is defined as a stock of population weighted by distance:
\[ A_i = \sum_{j=1}^n O_j f(d_{ij}) \]
The terms of this equation can be interpreted in a potential approach or an accessibility approach (in brackets):
- \(A_i\) is the potential at \(i\) (the accessibility)
- \(O_j\) is the stock of population at \(j\) (the number of opportunities)
- \(f(d_{ij})\) is a negative function of the distance between \(i\) and \(j\), mainly of the power or the exponential form.
The computation of potentials could be considered as a spatial interpolation method such as inverse distance weighted interpolation (IDW) or kernel density estimator (KDE). These models aim to estimate unknown values of non-observed points from known values given by measure points. Cartographically speaking, they are often used to get a continuous surface from a set of discrete points. However, we argue that the Stewart model is mainly a spatial interaction modeling approach, with a possible secondary use for spatial interpolation.
The distance friction
Modeling spatial interactions implies quantifying the distance friction or impedance. The role of the distance can be interpreted as a disincentive to access desired destinations or opportunities (e.g. jobs, shops). At the very place of the opportunity, the interaction function equals 1, meaning that the potential access is 100%. Far away from the opportunity, the interaction function tends to 0, meaning that the potential access is 0 %. The span is defined as the value where the interaction function falls to 0.5 (50%). From the individuals’ point of view, this function may be seen as a degree of availability of a given opportunity. From the opportunity’s point of view (a store for example), the interaction function may be seen as a decreasing catchment area: there is a maximal attraction close to the opportunity and this attraction decreases progressively through distance.
Examples
Potential in one point
The first example details the steps involved in the computation of the potential for one point (\(A_{i=1}\)). This example is based on a population dataset of administrative units of the French region of Occitanie. The stocks of population (\(O_j\)) are located on the centroids of the regions.
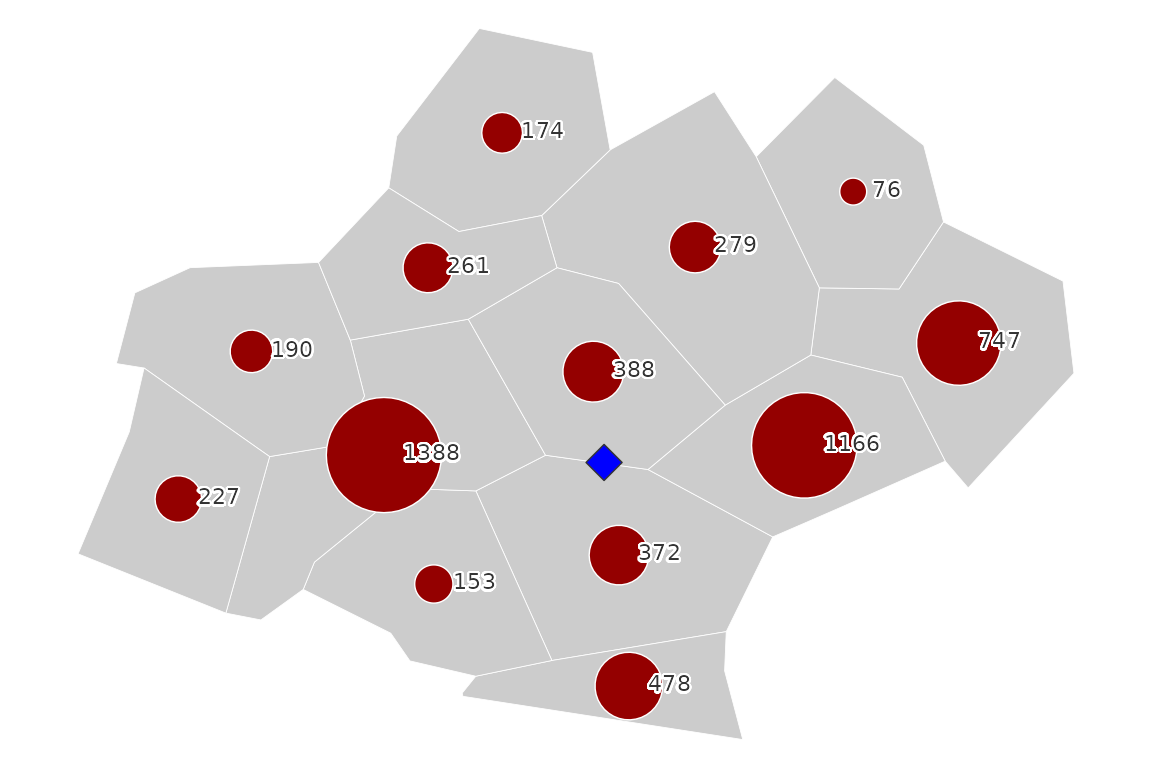
\(O_j\) and \(_i\)
The first step is computing the distances between the point and all population places.
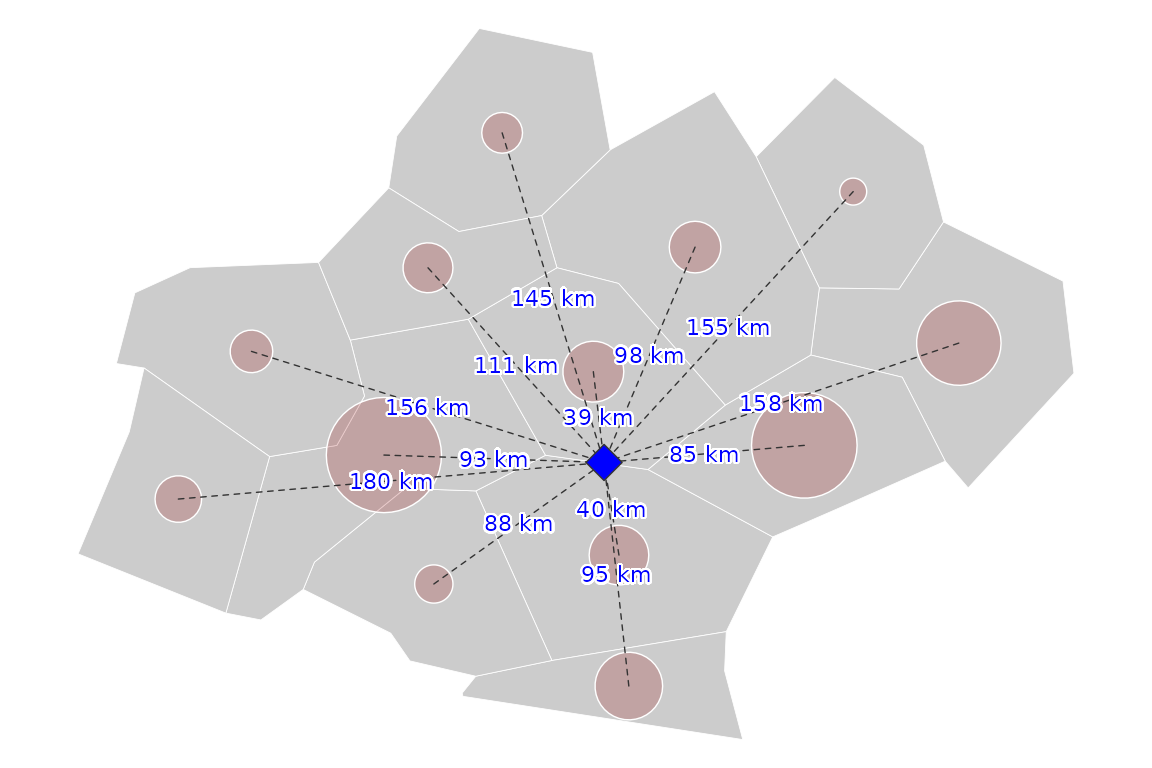
\(d_{ij}\)
For the next step we have to select a distance friction function.
plot_inter() allows to visualize the decrease of the
interaction intensity with the distance according to the selected
function and its parameters.
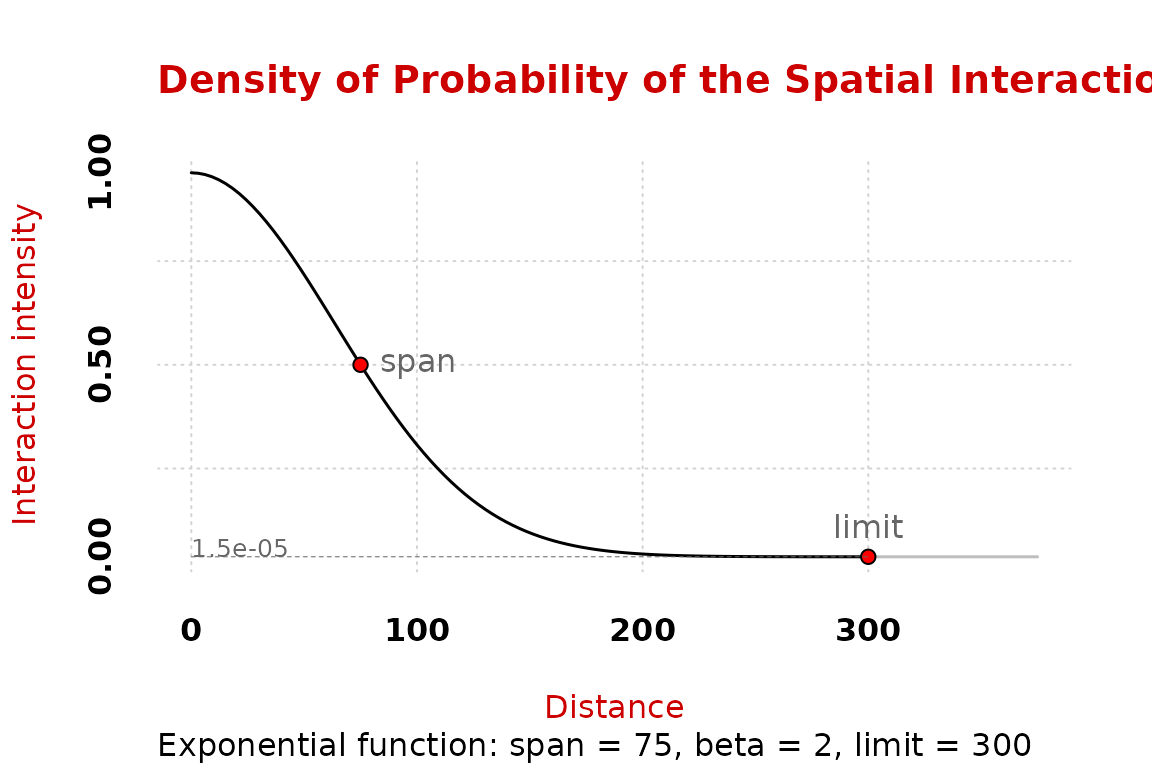
\(f(d_{ij})\)
Here, the probability of interaction at the span value (75 km) is 0.5.
We can now use the values of the interaction intensity for each distance between \(i\) and \(j\).
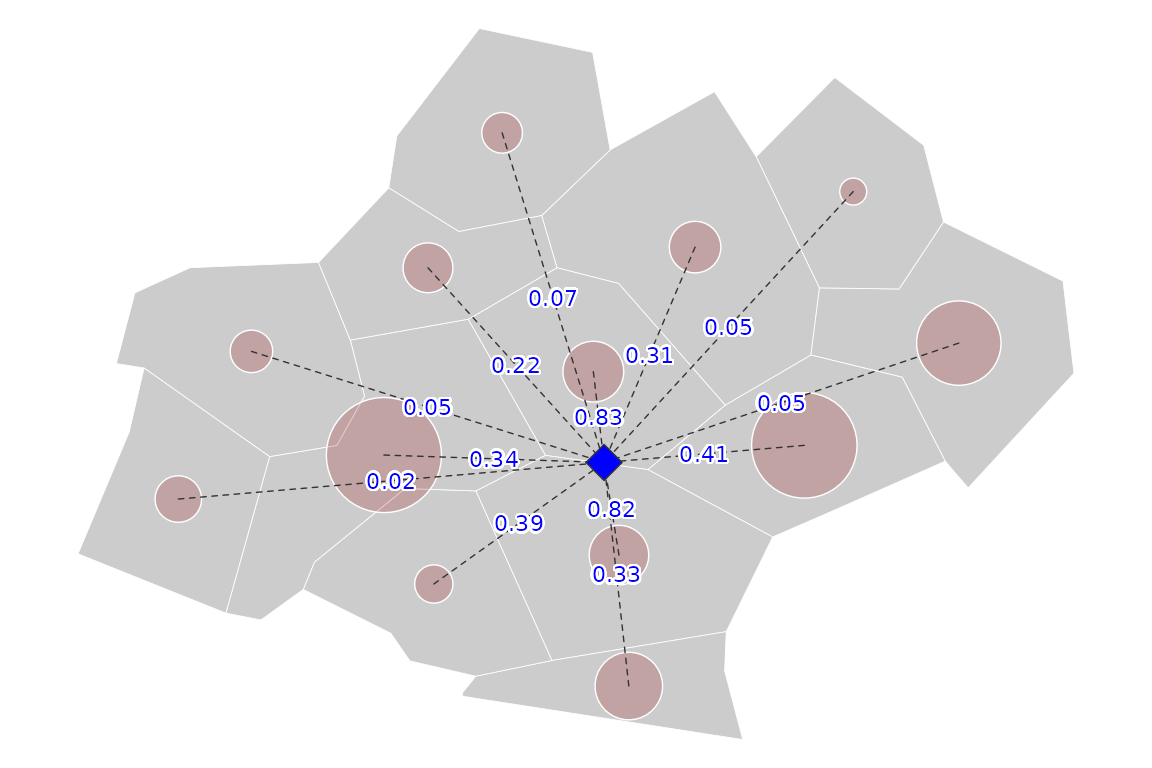
\(f(d_{ij})\)
The contribution of each \(j\) to the total potential (\(A_i\)) is equal to the interaction intensity multiplied by its mass (\(O_j f(d_{ij}\)).
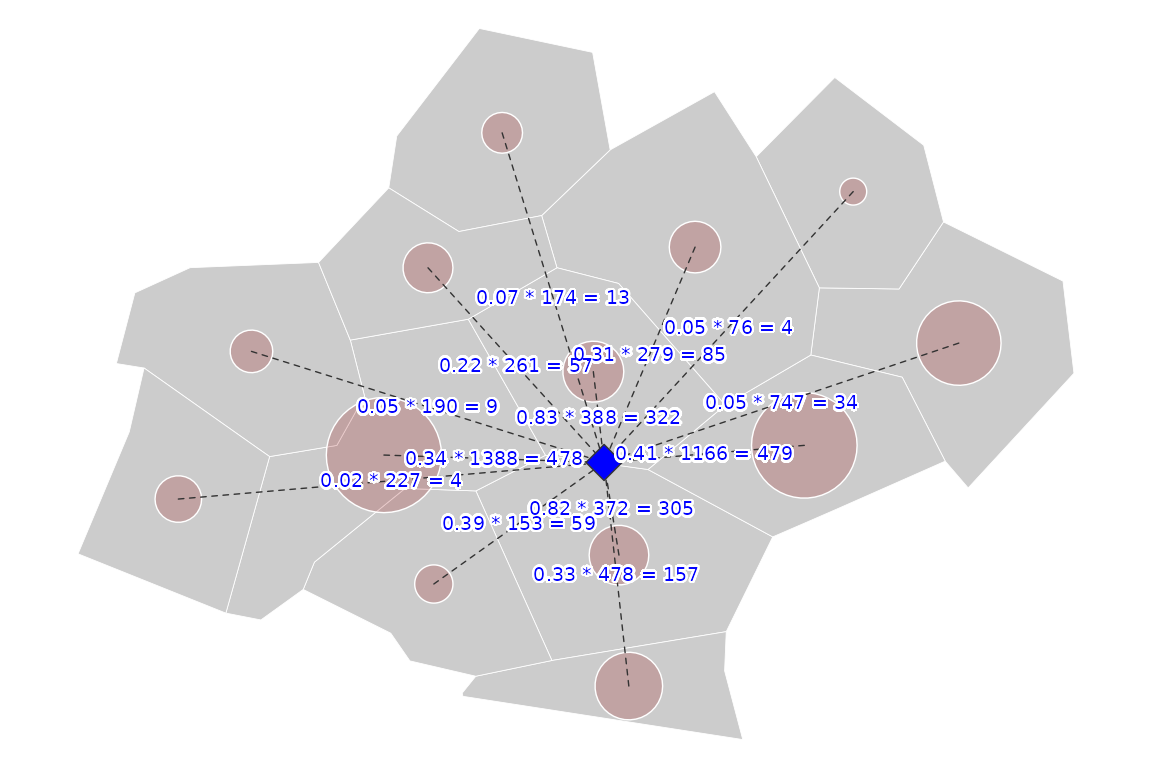
\(O_j f(d_{ij})\)
It can be rendered cartographically in the following figure.
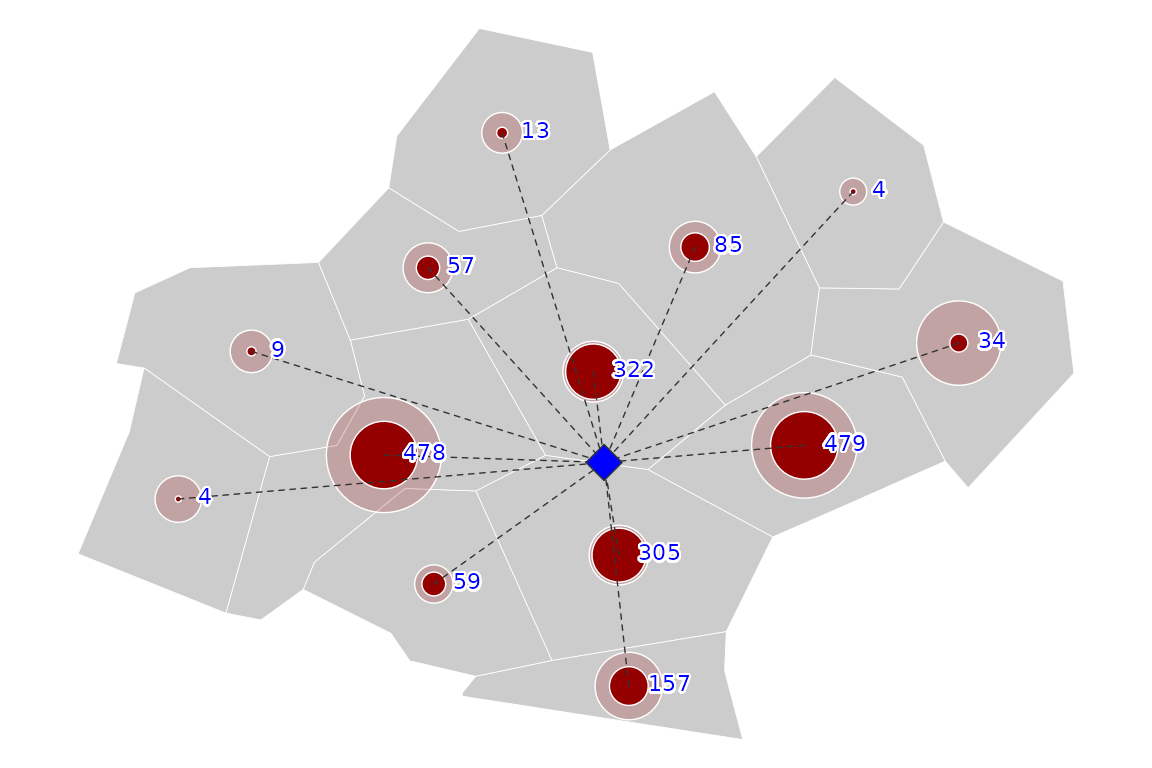
\(O_j f(d_{ij})\)
Finally, the value of the potential of \(i\) is the sum of each \(j\)’s contributions.
Potentials in a pseudo-continuous space
A common practice is to compute potentials on points of a regular grid to estimate potentials on a pseudo-continue surface.
We can use the same dataset as an example of use.
Create a regular grid
create_grid() is used to create a regular grid with the
extent of an existing layer (x) and a specific resolution
(res). The resolution is set in units of x
(here, meters).
library(potential)
library(mapsf)
mf_map(n3_poly, col= "grey80", border = "white", lwd = .4)
y <- create_grid(x = n3_poly, res = 100000)
mf_map(y, pch = 23, add = TRUE, bg = "blue", cex = .5 )
Create a distance matrix
create_matrix() is used to compute distances between
objects.
d <- create_matrix(x = n3_pt, y = y)
d[1:5, 1:5]
#> 1 2 3 4 5
#> 1 2674796 2578559 2482621 2387015 2291785
#> 2 2622868 2526551 2430532 2334847 2239539
#> 3 2682813 2587272 2492081 2397282 2302922
#> 4 2643075 2547108 2451462 2356179 2261302
#> 5 2638427 2542933 2447799 2353068 2258792The distance is expressed in map units (meters).
Compute the potentials
The potential() function computes potentials.
y$pot <- potential(x = n3_pt, y = y, d = d,
var = "POP19", fun = "e",
span = 75000, beta = 2)
mf_map(n3_poly, col= "grey80", border = "white", lwd = .4)
mf_map(y, var = "pot", type = "prop",
inches= .1,
lwd = .5,
leg_val_cex = .5,
leg_val_rnd = -3,
leg_frame = TRUE,
leg_pos = "topright")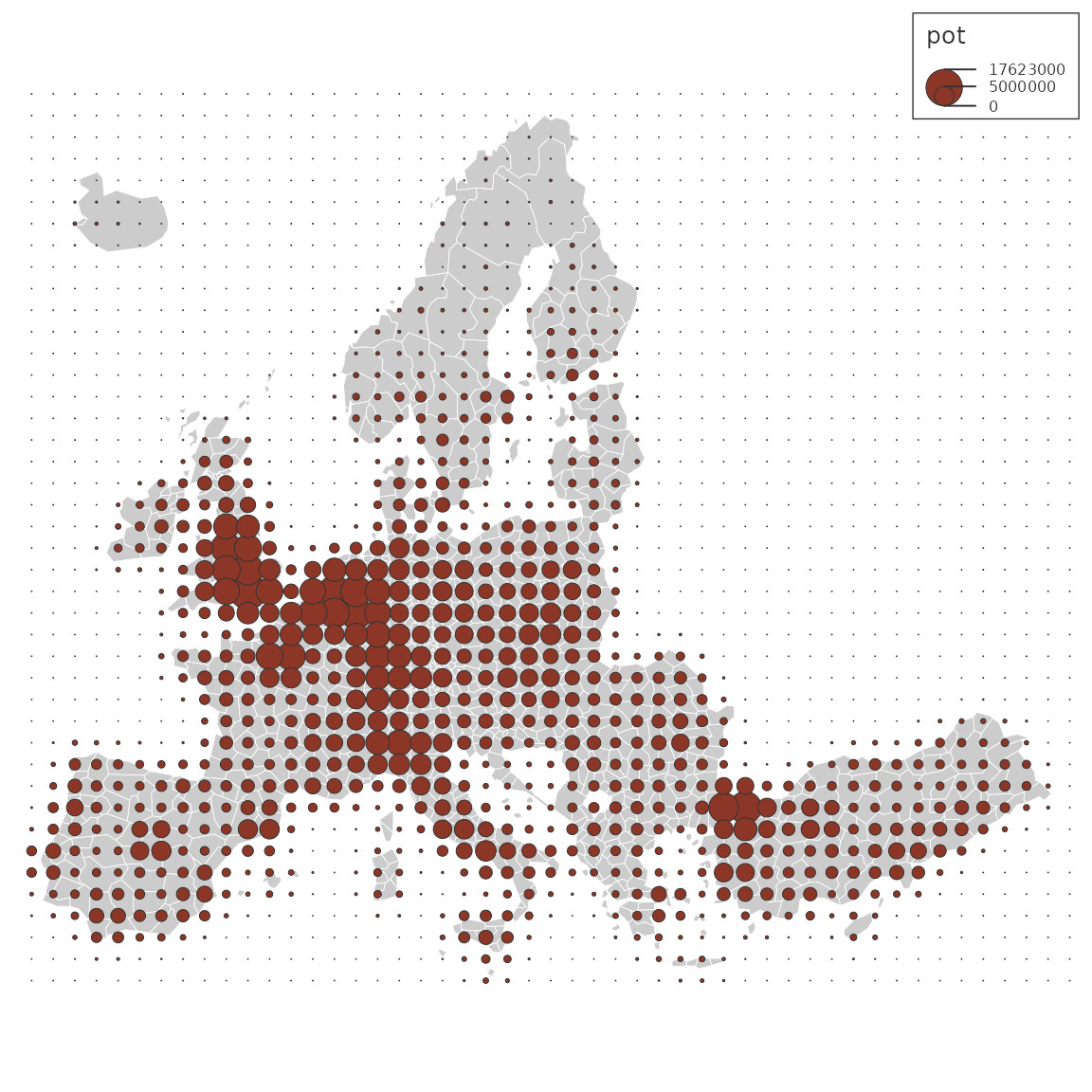
It’s possible to express the potential relatively to its maximum in order to display more understandable values (Rich 1980).
y$pot2 <- 100 * y$pot / max(y$pot)
mf_map(n3_poly, col= "grey80", border = "white", lwd = .4)
mf_map(y, var = "pot2", type = "prop",
inches= .1,
lwd = .5,
leg_val_cex = .5,
leg_val_rnd = 0,
leg_frame = TRUE,
leg_pos = "topright")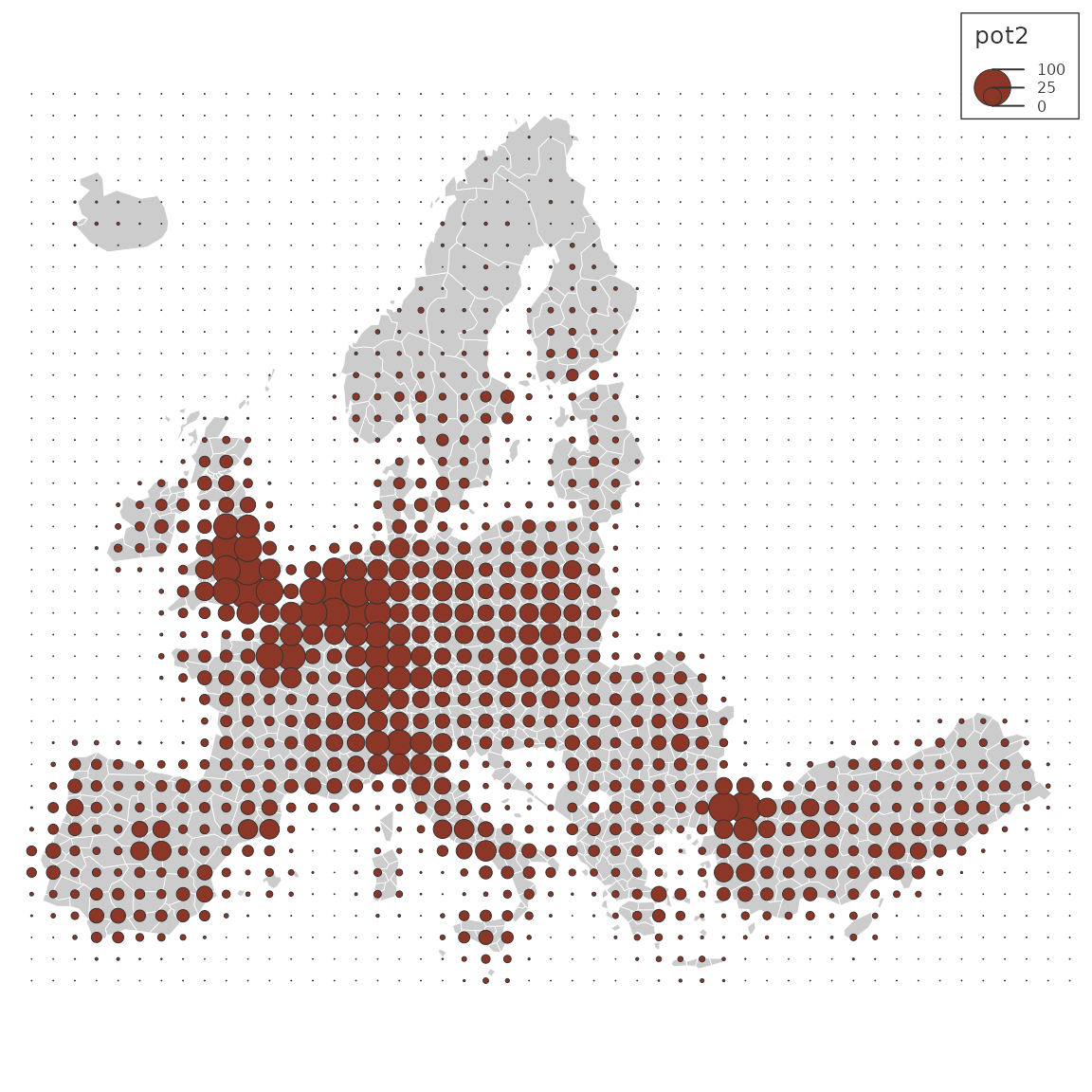
It’s also possible to compute areas of equipotential with
equipotential().
bks <- seq(0, 100, 10)
iso <- equipotential(x = y, var = "pot2", breaks = bks, mask = n3_poly)
mf_map(x = iso, var = "min", type = "choro",
breaks = bks,
pal = hcl.colors(10, 'Teal'),
lwd = .2,
border = "#121725",
leg_pos = "topright",
leg_val_rnd = 0,
leg_title = "Potential of\nPopulation")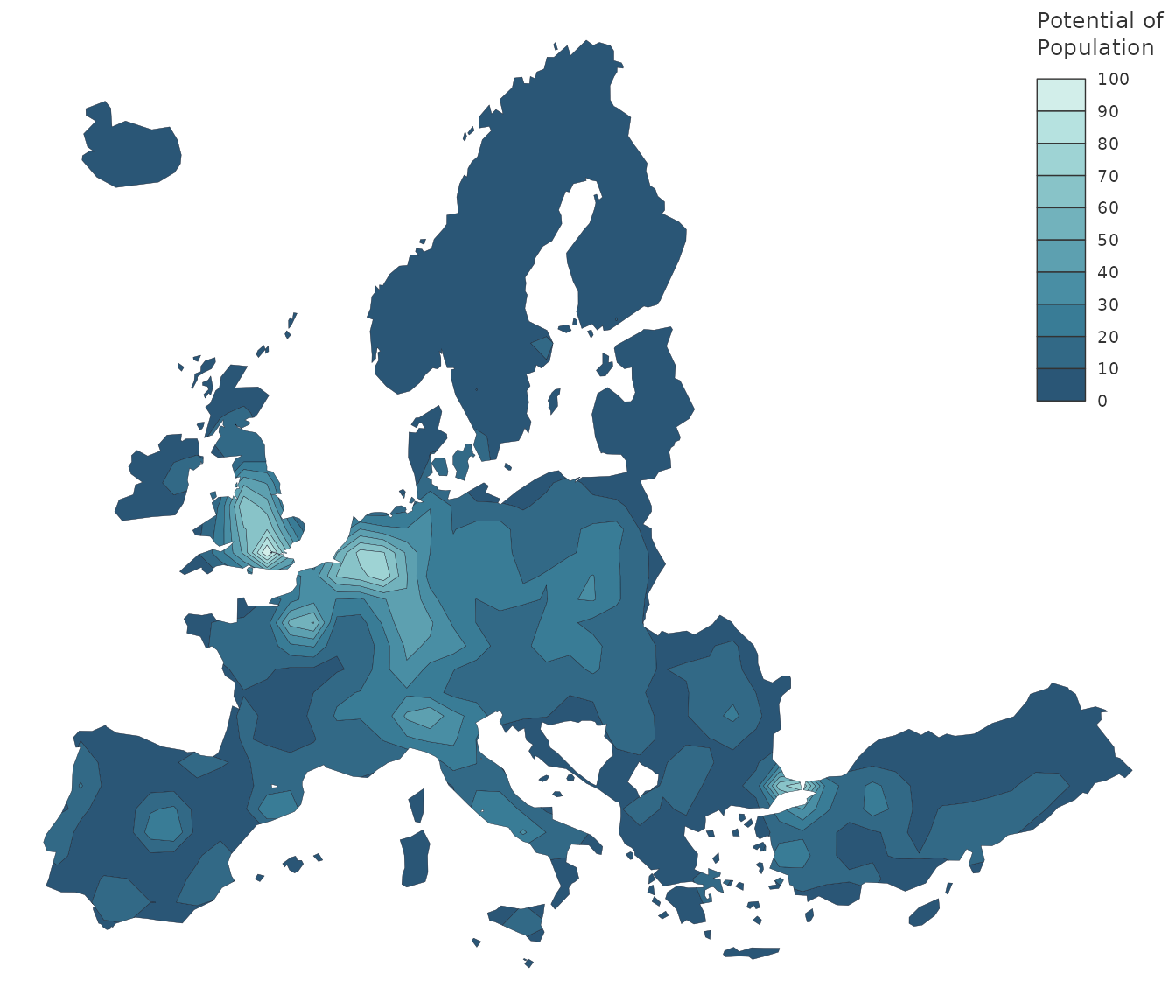
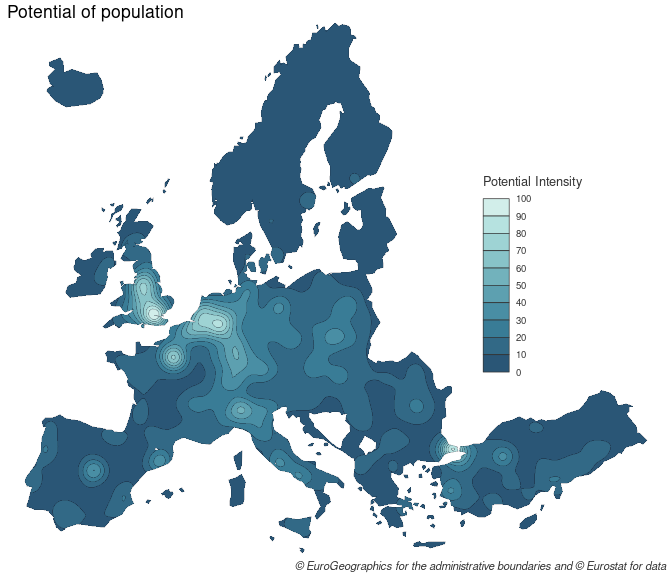
Compute the potentials using parallel computation
In order to obtain smoother equipotential areas we need to compute
the potentials on a much finer grid and that can be really time
consuming with potential().mcpotential() computes potentials with a cutoff distance
and parallel computation. The cutoff distance means that points that are
too far away are not taken into account in the computation. The limits
of this function are the impossibility to provide custom distance
matrices (d), and the fact that it only uses Cartesian
distances (hence its use for global data is likely to be
inappropriate).
y <- create_grid(x = n3_poly, res = 20000)
y$pot <- mcpotential(x = n3_pt, y = y,
var = "POP19", fun = "e",
span = 75000, beta = 2,
limit = 200000, ncl = 2)
y$pot2 <- 100 * y$pot / max(y$pot)
bks <- seq(0, 100, 10)
iso <- equipotential(x = y, var = "pot2", breaks = bks, mask = n3_poly)
mf_map(x = iso, var = "min", type = "choro",
breaks = seq(0,100, 10),
pal = hcl.colors(10, 'Teal'),
lwd = .2,
border = "#121725",
leg_pos = c(6084270,4253383),
leg_val_rnd = 0,
leg_title = "Potential Intensity")
mf_credits(txt = "© EuroGeographics for the administrative boundaries and © Eurostat for data",
pos = "bottomright", cex = .7)
mf_title(txt = "Potential of population", bg = "white", fg = "black", inner = TRUE, cex = 1.1)